112 學測數Ａ - 選填題 第 17 題

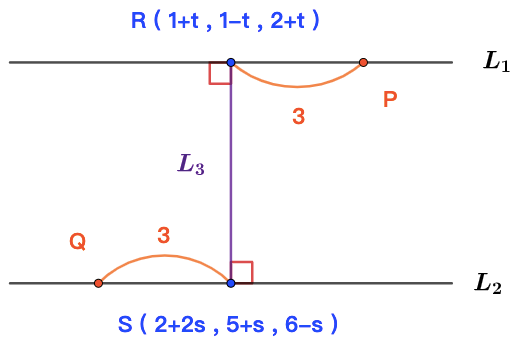
$令 \ \overrightharpoon{n_1} \ 為 \ L_1 \ 之方向向量 \ , \ \overrightharpoon{n_2} \ 為 \ L_2 \ 之方向向量 \ , \ 則 : \\ \ \\ \begin{aligned} & \overrightharpoon{RS} \ / / \ \overrightharpoon{n_1} \ \times \ \overrightharpoon{n_2}=\left(\ \left|\begin{array}{rr} -1 & 1 \\ 1 & -1 \end{array}\right|\ , \ \left|\begin{array}{rr} 1 & 1 \\ -1 & 2 \end{array}\right| \ , \ \left|\begin{array}{rr} 1 & -1 \\ 2 & 1 \end{array}\right|\ \right)=(\ 0\ ,\ 3\ ,\ 3\ ) \\ \ \\ & (\ 2 s-t+1\ , \ s+t+4\ ,\ -s-t+4\ )\ // \ (\ 0\ ,\ 1\ ,\ 1\ ) \ \ , \ \ \underline{\ s=-\frac{1}{3} \ , \ t=\frac{1}{3}\ } \\ \ \\ \ \\ & R\left(\ \frac{4}{3} \ , \ \frac{2}{3} \ , \ \frac{7}{3}\ \right) \ , \ S\left(\ \frac{4}{3} \ , \frac{14}{3}\ , \frac{19}{3}\ \right) \\ \ \\ & P=R+\frac{\ 3}{\sqrt{3\ }\ } \ (\ 1\ ,\ -1\ ,\ 1\ ) \ \ , \ \ Q=S+\frac{\sqrt{6\ }}{\ \ 2}\ (\ 2\ ,\ 1\ ,\ -1\ ) \\ \ \\ & P=\left( \ \frac{4}{3}+\sqrt{3} \ , \ \frac{2}{3}-\sqrt{3} \ , \ \frac{7}{3}+\sqrt{3}\ \right) \ , \ Q=\left(\ \frac{4}{3}+\sqrt{6} \ , \ \frac{14}{3}+\frac{\sqrt{6}}{2} \ , \ \frac{19}{3}-\frac{\sqrt{6}}{2}\ \right) \end{aligned} \\ \ \\ \ \\ 由兩點距離公式得：\ \underline{\ \overline{P Q}=5 \sqrt{2}\ } \ \ _\#$

觀念說明：

   這一題算是難度偏高的題目！

   首先這題的計算量很大，在考試壓力下要完整解出這題不容易，

   平時就要有很扎實的運算實力才有辦法做到

   分析題目也是這題的關鍵之一，

   \( L_3 \) 同時垂直於 \( L_1 \) 和 \( L_2 \)，要能夠聯想到公垂向量，然後利用外積把公垂向量解出來

   R、S 點求出來之後再利用單位向量的觀念，把 P、Q 兩點也找出來，

   最後用兩點距離公式算出 \( \overline{PQ} \) 的長度

   這題步驟多、計算複雜，在解題時必須要有耐心，相信自己一定能夠算得出來 💪🏻

• 如果有線上教學的需求，歡迎到我的 AmazingTalker 頁面上進行預約：

Allen老師 🏅 北大台中一中畢業 | 資深高中數學補習班講師 經認證的數學線上教師

💎 十年教學經驗，在職補習班數學講師💎 北大＋台中一中畢業，教學資優生最在行💎 基測 PR99，學測數學 15 級分，考試技巧一把抓 💎 教授學生超過百位，教學經驗滿分💎 一對一家教、小團班、大團班皆有授課經歷💎 專業解析學校小考、段考題，讓您準備學校考試不用擔心💎 擅長深入潛出，用最簡單的方式講解最困難的數學💎 引導式教學：一步一步帶領學生寫出算式、找出答案💎 找出弱點、加強不會的單元，對症下藥最有效！💎 優化解題流程、提供最佳算法，讓您考試不用擔心時間壓力💎 學測、分科測驗、國中會考複習班開課中，歡迎試聽！

AmazingTalkerAmazingTalker

( 評論區需要註冊才能留言，為系統內建設定

 註冊和留言完全免費，有問題可以在底下發問，我會盡力回覆！)