112 學測數Ａ - 單選題 第 6 題

首先我們必須知道「期望值」的算法：期望值 ＝ 機率  X  數值

再來我們分析每一種情況的機率與其內積之後得到的數值

由於題目給的是正立方體，而且邊長為 1，非常適合坐標化來解題，

我們可以建立一個坐標系，令 O 為原點，會得到以下的結果：

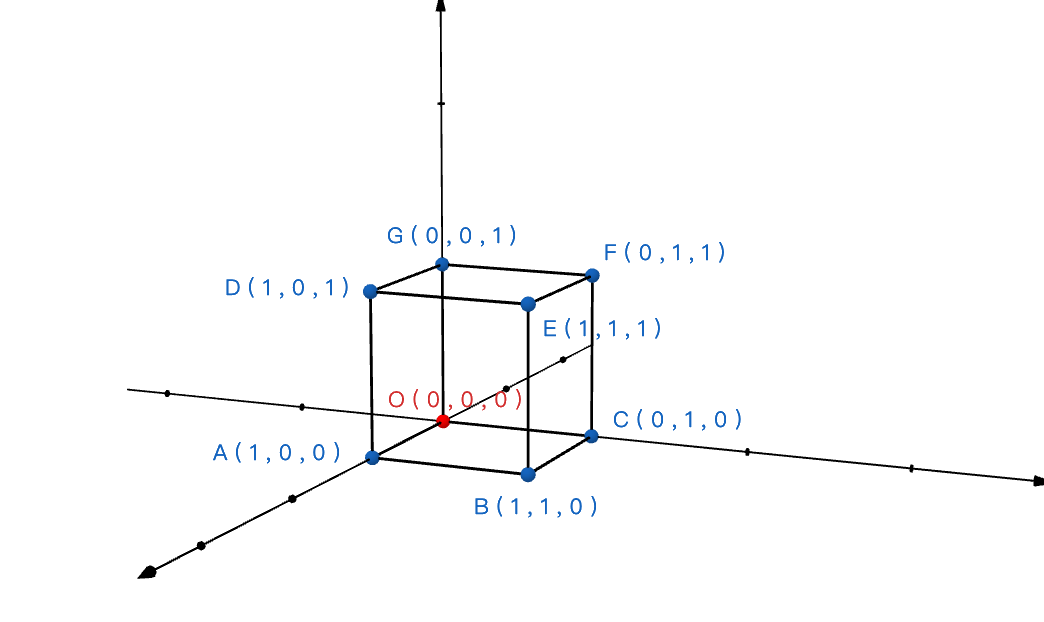
其中 $\left | \overrightharpoon {OP} \right |$、$\left | \overrightharpoon {OQ} \right |$ 可能有三種長度，分別為 1、$\sqrt{2}$、$\sqrt{3}$

1. $\left| \overrightharpoon {OP} \right|$ = $\left| \overrightharpoon {OQ} \right|$ = 1

P、Q 為 A、G、C 三點任取兩點，P、Q可交換

其機率為：$\dfrac{C_{2}^{3}\times 2!}{C_{2}^{7}\times 2!} = \dfrac{6}{42} = \dfrac{1}{7}$ ， 其內積數值為：$1\cdot 1\cdot \cos 90^{\circ }=0$

期望值：$\dfrac{1}{7} \times 0 = 0$

2. $\left| \overrightharpoon {OP} \right| = 1$ , $\left| \overrightharpoon {OQ} \right| = \sqrt{2}$ or $\left| \overrightharpoon {OP} \right| = \sqrt{2}$ , $\left| \overrightharpoon {OQ} \right| = 1$

這種情況下有兩種內積的數值，

第一種：夾角 $45^{\circ }$，即 ( P , Q ) = ( G , F ) , ( F , C ) , ( C , B ) , ( B , A ) , ( A , D ) , ( D , G )

其中 P、Ｑ 可交換，故共有 6 X 2 = 12 種情形

機率為：$\dfrac {12}{42} = \dfrac {2}{7}$ ， 內積數值為：$1\cdot \sqrt{2}\cdot \cos 45^{\circ } = 1$

期望值為：$\dfrac {2}{7} \times 1 = \dfrac {2}{7}$

第二種：夾角 $90^{\circ }$，即 ( P , Q ) = ( G , B ) , ( C , D ) , ( A , F )

其中 P、Ｑ 可交換，故共有 3 X 2 = 6 種情形

機率為：$\dfrac {6}{42} = \dfrac {1}{7}$ ， 內積數值為：$1\cdot \sqrt{2}\cdot \cos 90^{\circ } = 0$

期望值：$\dfrac {1}{7} \times 0 = 0$

3. $\left| \overrightharpoon {OP}\right| =1$ , $\left| \overrightharpoon {OQ}\right| = \sqrt{3}$ or $\left| \overrightharpoon {OP}\right| =\sqrt{3}$ , $\left| \overrightharpoon {OQ}\right| = 1$

P、Q 為 A、G、C 三點任取一點，搭配 Ｅ點，P、Q可交換

機率為：$\dfrac{c_{1}^{3}c_{1}^{1}\cdot 2!}{42}=\dfrac{6}{42}=\dfrac{1}{7}$ ，

內積為：$\left( 0,0,1\right) \cdot \left( 1,1,1\right) =1$ ( 6 種情形內積結果皆同，拿 $\overrightharpoon {OG} \cdot \overrightharpoon {OE}$ 來做計算 )

期望值：$\dfrac{1}{7} \times 1 = \dfrac{1}{7}$

4. $\left| \overrightharpoon {OP}\right| = \left| \overrightharpoon {OQ}\right| = \sqrt{2}$

P、Q 為 D、F、B 三點任取兩點，P、Q可交換

機率為：$\dfrac{c_{2}^{3}\cdot 2!}{42}=\dfrac{6}{42}=\dfrac{1}{7}$ ，內積為：$\sqrt{2} \cdot \sqrt{2} \cdot \cos 60^{\circ }=1$

期望值：$\dfrac{1}{7} \times 1 = \dfrac{1}{7}$

5. $\left| \overrightharpoon {OP}\right| = \sqrt{2}$ , $\left| \overrightharpoon {OQ}\right| = \sqrt{3}$ or $\left| \overrightharpoon {OP}\right| =\sqrt{3}$ , $\left| \overrightharpoon {OQ}\right| = \sqrt{2}$

P、Q 為 D、F、B 三點任取一點，搭配 Ｅ點，P、Q可交換

機率為：$\dfrac{c_{1}^{3}c_{1}^{1}\cdot 2!}{42}=\dfrac{6}{42}=\dfrac{1}{7}$ ，

內積為：$\left( 1,0,1\right) \cdot \left( 1,1,1\right) =2$ ( 6 種情形內積結果皆同，拿 $\overrightharpoon {OD} \cdot \overrightharpoon {OE}$ 來做計算 )

期望值：$\dfrac{1}{7} \times 2 = \dfrac{2}{7}$

把所有情形的期望值全部加起來，得到：$0+\dfrac{2}{7}+0+\dfrac{1}{7}+\dfrac{1}{7}+\dfrac{2}{7}=\dfrac{6}{7}$ ，

答案選 ( 3 )

觀念說明：

    這一題偏複雜，雖然計算不難，但是討論各種情形的時候很容易漏掉。

    在討論排列組合、機率、期望值等題目時，盡量要有條理、有系統地來討論，

    例如我這邊是利用向量長度來區分各種情形做探討，

    當然本題不限於這個方法，但務必找到一個可以完整討論所有情形的分類方式。

• 如果有線上教學的需求，歡迎到我的 AmazingTalker 頁面上進行預約：

Allen老師 🏅 北大台中一中畢業 | 資深高中數學補習班講師 經認證的數學線上教師

💎 十年教學經驗，在職補習班數學講師💎 北大＋台中一中畢業，教學資優生最在行💎 基測 PR99，學測數學 15 級分，考試技巧一把抓 💎 教授學生超過百位，教學經驗滿分💎 一對一家教、小團班、大團班皆有授課經歷💎 專業解析學校小考、段考題，讓您準備學校考試不用擔心💎 擅長深入潛出，用最簡單的方式講解最困難的數學💎 引導式教學：一步一步帶領學生寫出算式、找出答案💎 找出弱點、加強不會的單元，對症下藥最有效！💎 優化解題流程、提供最佳算法，讓您考試不用擔心時間壓力💎 學測、分科測驗、國中會考複習班開課中，歡迎試聽！

AmazingTalkerAmazingTalker

( 評論區需要註冊才能留言，為系統內建設定

 註冊和留言完全免費，有問題可以在底下發問，我會盡力回覆！)